Implementation of high-performance GPU kernels in Nektar++

Implementation of high-performance GPU kernels in Nektar++

Due to the recent evolution of high performance computing hardware from single-core central processing units (CPUs) to multi-core CPUs and the emergence of general purpose graphics processing units (GPGPUs or short GPUs), these shared memory systems are now characterised by a high degree of parallelism. They also possess a variety of architecture-specific features that must be appropriately utilised in order to fully realise their capabilities.

In the context of high-order finite element methods, and specifically within the Nektar++ framework, the efficiency of core operators for compressible and incompressible Navier-Stokes solvers has already been optimised using SIMD vectorisation on CPUs (see https://prism.ac.uk/2020/04/blog-entry-improving-the-performance-of-nektar-with-simd/, based on the work of Moxey et al., 2020).

Now we optimise the same core operators, but targetting GPUs, using the native CUDA programming model. We investigate two types of efficient CUDA kernels for a range of polynomial orders and thus varying arithmetic intensities; a first type which maps each elemental operation to a CUDA-thread for a completely vectorised kernel, and a second that maps each element to a CUDA-block for nested parallelism. For both options we show the importance of the right layout of data structures, which necessitates the development of interleaved elemental data for vectorised kernels, and additionally analyse the effect of utilising GPU-specific memory spaces. As the considered kernels are foremost memory bandwidths bound, we develop kernels for curved elements that trade memory bandwidths against additional arithmetic operations, and demonstrate improved throughput for low polynomial orders.

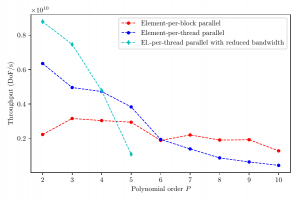
Figure Caption: Throughput of the Helmholtz operator for curved triangular elements over a range of polynomial orders, measured on a Nvidia Titan V GPU. Depending on the polynomial order, and thus the arithmetic intensity of the kernel, different types of kernels show the highest performance.